[이산수학]논리연산자란?(부정, 논리곱, 논리합, 배타적 논리합)_진리표로 나타내기

[이산수학]논리연산자란?(부정, 논리곱, 논리합, 배타적 논리합)_진리표로 나타내기

 

명제는 두 개 이상 결합하여 사용됩니다. 이 때 논리 연산자를 이용하는데 부정, 논리곱, 논리합, 배타적 논리합이 있습니다.

 

여러 명제를 합친 결과를 비교할 때 유용한 '진리표(Truth Table)'가 있습니다. 명제에서 나올 수 있는 참/거짓 판단의 모든 가능성을 표로 나열하였습니다. 예로 단순 명제 p의 진리표는 다음과 같습니다. 

※ 단순 명제: 더 이상 나눌 수 없는 명제 

 

p

T(True, 참)

F(False, 거짓)

 

이제 명제의 결합 중에 어떤 것이 있는지 보고, 이해를 위해 진리표와 밴다이어그램도 다루겠습니다.   

 

■ 부정 (Negation) NOT

명제 p를 부정

 

예) 오늘 새로운 메뉴가 나온다.

->오늘 새로운 메뉴가 나오는 것은 사실이 아니다

->오늘 새로운 메뉴가 안 나온다. 

 

부정 진리표/밴다이어그램

 

※ 모든(all)과 어떤(any)의 부정 (헷갈림 주의!)

'모든 사람은 똑똑하다'의 부정은?

'모든 사람은 똑똑하지 않다'가 아니라,

 

- 모든 사람이 똑똑한 것은 사실이 아니다.

- 어떤 사람은 똑똑하지 않다.

- 똑똑하지 않은 사람이 하나라도 있다. 

 

확인문제

'어떤 사람은 똑똑하다'의 부정은?

답은 글 맨 아래에서 확인 

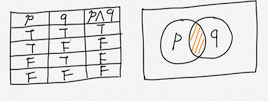
■ 논리곱 (Conjunction) AND

명제 p와 q가 있을 때, 둘 다 참일 때만 참

그렇지 않으면 거짓 즉, 두 조건을 다 만족해야 한다. 

 

예)

흰 차의 주 판매량은 100대이다.

검은 차의 주 판매량은 110대이다. 

 

->흰 차의 주 판매량은 100대이고, 검은 차의 주 판매량은 110대이다. 

 

논리곱 진리표/밴다이어그램

 

 

■ 논리합(Disjunction) OR

명제 p와 q가 있을 때, 하나라도 참이면 참, 그렇지 않으면 거짓

기호 +도 쓸 수도 있다. 

 

->흰 차의 주 판매량은 100대이거나, 검은 차의 주 판매량은 110대이다. 

 

논리합 진리표/밴다이어그램

 

■ 배타적 논리합(Exclusive OR) XOR

명제 p와 q가 있을 때, 하나만 참이면 참

꼭 하나만!! 둘이면 안됨. 

둘 다 같으면 거짓, 다르면 참

 

->흰 차의 주 판매량은 100대가 아니고, 검은 차의 주 판매량은 110대가 아니다. 

 

 

배타적 진리표/밴다이어그램

 

 

 

확인문제 답

- 어떤 사람이 똑똑한 것은 사실이 아니다

- 모든 사람은 똑똑하지 않다. 

 

 

-----------------------------------

이산수학 총정리

목록 보러가기 

-----------------------------------