반응형
1이 실수에서 곱셈에 대한 항등원이듯 단위행렬은 행렬에서 곱셈에 대한 항등원이다.
주대각선 성분이 모두 1이고 나머지 성분이 모두 0인 n차 정사각행렬을 n차 단위행렬(identity matrix)이라고 한다. n차 단위 행렬은 아래와 같이 나타낸다.

A가 m X n 행렬일 때, 다음이 성립된다.
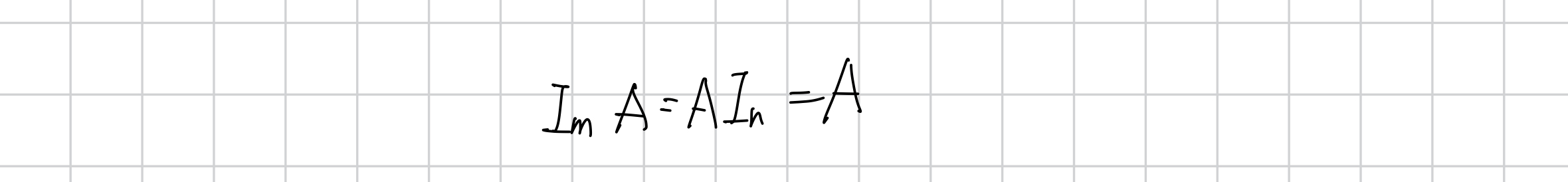
반응형
'컴퓨터 공학 > Software Math' 카테고리의 다른 글
| [선형대수학] 역행렬 (inverse matrix)의 성질 (0) | 2023.10.20 |
|---|---|
| [선형대수학] 가역행렬(invertible matrix) / 비가역행렬(noninvertible matrix) / 역행렬 (inverse matrix)란? (0) | 2023.10.20 |
| [선형대수학] 행렬 연산의 성질 (0) | 2023.10.20 |
| [선형대수학] 행렬의 곱(multiplication) AB 구하는 법 (0) | 2023.10.20 |
| [선형대수학] 행렬의 합(sum)과 스칼라 배(scalar multiplication)이란? (0) | 2023.10.20 |



댓글