[이산수학]최소신장 트리 구하는 프림 알고리즘(Prim Algorithm)이란?_예제포함
최소신장 트리(Minimal Spanning Tree)란 '그래프 G의 꼭짓점을 모두 노드로 포함하면서 비용을 최소로 하는 트리 T'입니다. 그래서 최소신장 트리를 구하기 위해서는 다음 두 가지 요소가 있어야 합니다.
1. 노드와 노드를 연결하는 변에 가중치에 부여된 그래프
2. 비용이 최소인 트리로 만들기 위한 알고리즘
2번의 알고리즘에는 프림 알고리즘(Prim Algorithm)과 크루스칼 알고리즘(Kruskal Algorithm)이 있습니다.
이 글에서는 프림 알고리즘에 대해 알아보겠습니다.
■ 프림 알고리즘(Prim Algorithm)
그래프 G의 변 중 비용이 가장 낮은 변들로 트리를 구성하는 알고리즘
(1) 가중치가 가장 작은 변을 선택
(2) 연결된 꼭짓점들과 연결된 모든 변들 중 가중치가 가장 작은 변을 선택
(3) 가중치가 같은 변은 임의로 선택
(4) 선택된 변에 대해 순환이 형성되는 경우는 선택하지 않음
(5) n개의 꼭짓점에 대하여 n - 1개의 변이 연결되면 종료
※ 순환(Cycle): 경로의 시작점과 끝이 같은 경우
■ 프림 알고리즘(Prim Algorithm) 예
다음 가중치가 있는 그래프를 프림 알고리즘을 이용해 최소신장 트리로 만들어봅시다.
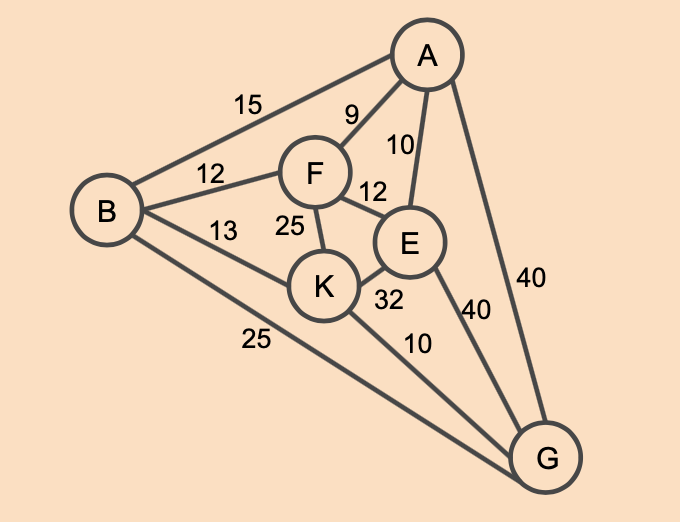
(1) 변에 부여된 비용 중 가장 작은 9를 선택하면 노드 A와 F가 연결됩니다. (노드 수 2, 가지 수 1)
(2) 노드 A와 F에 연결된 변들과 노드들은 다음 점선으로 표시된 것과 같습니다.
(3) (2)의 점선 중 비용이 가장 낮은 10을 선택하면 노드 A와 E가 연결됩니다. (노드 수 3, 가지 수 2)
(4) 노드 A, E, F에 연결된 변들과 노드들은 다음 점선으로 표시된 것과 같습니다.
(5) (4)의 점선 중 비용이 가장 낮은 변은 F와 E가 연결된 12와 F와 B가 연결된 12입니다. 이때 F와 E가 연결된 변은 노드 A, F, E간의 회로를 만들게 되므로 사용하지 않는다. (노드 수 4, 가지 수 3)
(6) 노드 A, B, E, F에 연결된 변들과 노드들은 다음 점선으로 표시된 것과 같습니다. (5)에서 회로가 생성되는 것을 확인했으므로 F와 E를 연결하는 변을 제거했습니다.
(7) (6)의 점선 중 비용이 가장 낮은 변은 B와 K가 연결된 13이다(노드 수 5, 가지 수 4)
(8) 노드 A, B, E, F, K에 연결된 변들과 노드들은 다음 점선으로 표시된 것과 같습니다.
(9) (8)의 점선 중 비용이 가장 낮은 변은 K와 G가 연결된 10이다(노드 수 6, 가지 수 5)
(10) 모드 노드를 연결한 최소신장 트리가 완성되었습니다. 이때 이 최소신장 트리의 비용은 다음과 같습니다.
9 + 10 + 12 +13 + 10 = 54
수학으로 이해하는 디지털 논리 이산수학 396p 참고
-----------------------------------
-----------------------------------
'컴퓨터 공학 > Software Math' 카테고리의 다른 글
| [이산수학]최소신장 트리란?/ 최소신장 트리 구하는 알고리즘 (1) | 2020.08.30 |
|---|---|
| [이산수학]최소신장 트리 구하는 크루스칼 알고리즘(Kruskal Algorithm) 이란? (1) | 2020.08.29 |
| [이산수학]이진 탐색 트리란?_예제포함 (0) | 2020.08.27 |
| [이산수학]이진트리 순회표기법의 종류(전위표기, 중위표기, 후위표기)_예제포함 (0) | 2020.08.26 |
| [이산수학]이진트리의 순회(전위순회, 중위순회, 후위순회) (0) | 2020.08.26 |



댓글