■ 부분 그래프(Subgraph)
그래프 G = (V, E)가 있을 때, V' ⊆ V 이고 E' ⊆ E인 그래프 G' = (V', E')
어떤 그래프 G가 있을 때 그래프에 포함되는 일부 꼭짓점과 변으로만 그린 그래프를 부분 그래프라고 합니다.
■ 부분신장 그래프(Spanning Graph)
그래프 G = (V, E)가 있을 때, V' = V 이고 E' ⊆ E인 그래프 G' = (V', E')
부분 그래프 중에서 그래프 G의 꼭짓점을 모두 포함한 부분 그래프를 부분신장 그래프라고 합니다.
예를 들어 그래프 G가 다음과 같이 정의되고 있다고 하면,
G = (V, E)
V = {(A, B, C, D)}
E = {(A, B), (A, D), (B, C), (C, D), (D, B)}
G 그래프, G의 부분 그래프, G의 부분신장 그래프를 그리면 다음과 같습니다.
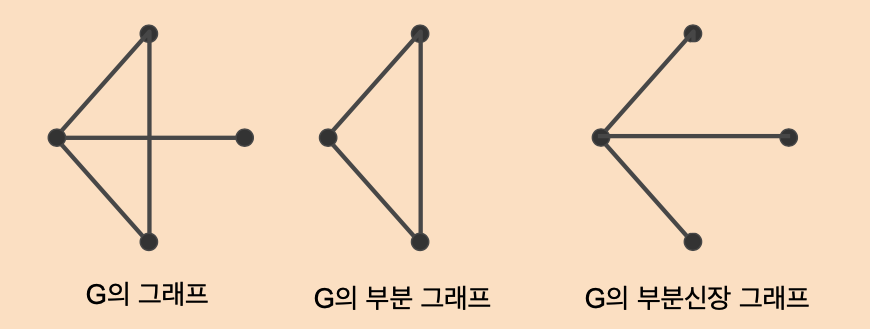
여기서 주의할 것은 부분 그래프나 부분신장 그래프는 반드시 G 그래프를 구성하는 꼭짓점과 변으로만 그려야 합니다. 위의 예에서는 G 그래프에 변 (A, C)가 존재하지 않으므로 부분 그래프나 부분신장 그래프에도 변 (A, C)를 그릴 수 없습니다.
■ 동형 그래프(Isomorphic Graph)
그래프 G = (V, E)와 G' = (V', E') 에 대해, 함수 f: V→ V'가 u,v ∈ V에 대해 (u, v) ∈ E ⇔ (f(u), f(v)) ∈ E' 인 전단사함수일 때 그래프 G = (V, E)와 G' = (V', E')는 동형 그래프
두 그래프가 똑같은 꼭짓점과 똑같은 변으로 구성되어 있다면, 두 그래프를 동형 그래프라고 합니다. 그래프를 구성하는 꼭짓점과 변이 같다면 다양한 형태의 동형 그래프가 존재할 수 있습니다.
예제
(1) ~ (2) 그래프가 다음 그래프와 동형 그래프인지 아닌지 판별하라
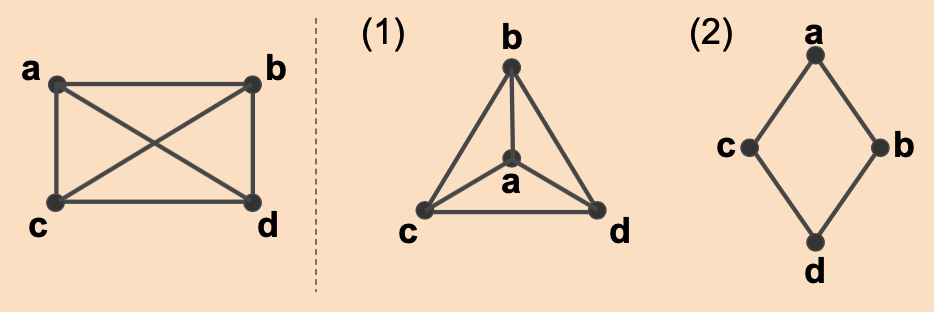
풀이
더보기를 클릭하세요.
예제풀이
(1)
동형 그래프이다.
(2)
동형 그래프 아니다.
■ 평면 그래프(Planar Graph)
그래프 G = (V, E)를 평면에 그릴 때, 꼭짓점이 아닌 곳에서는 어떤 변도 교차하지 않는 그래프
예제
다음 그래프에 대해 평면 그래프인 동형 그래프를 하나 그려라.
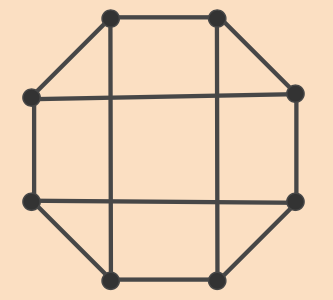
풀이
더 보기를 클릭하세요.
예제풀이
교차하는 변들을 교차하지 않도록 그리면 됩니다.

수학으로 이해하는 디지털 논리 이산수학 306p 참고
-----------------------------------
-----------------------------------
'컴퓨터 공학 > Software Math' 카테고리의 다른 글
| [이산수학]그래프의 종류2(연결 그래프, 완전 그래프, 정규 그래프, 이분 그래프) (0) | 2020.08.09 |
|---|---|
| [이산수학]오일러 그래프 정의와 정리(예제포함) (2) | 2020.08.09 |
| [이산수학]다중그래프, 방향그래프, 가중치그래프란?(예제포함) (0) | 2020.08.09 |
| [이산수학]그래프 개념과 용어 정리(루프, 경로, 회로, 인접)/예제포함 (0) | 2020.08.09 |
| [이산수학]함수의 종류(항등함수, 역함수, 상수함수, 특성함수, 바닥함수, 천정함수) (0) | 2020.08.08 |




댓글