이산수학_그래프의 종류2(연결 그래프, 완전 그래프, 정규 그래프, 이분 그래프) 예제로 이해하기
■ 연결 그래프(Connected Graph)
그래프 G = (V, E) 내에 있는 임의의 꼭짓점 u, v 간에 경로가 있는 그래프
예제
다음 중 연결 그래프인 것과 아닌 것을 구분하라.

풀이
예제풀이
(1)
그래프 안에 있는 모든 꼭지점 간에 경로가 존재한다. 예를 들어 e에서 d로 가는 경로는 e - b- c - a- f - b - d다.
∴ 연결그래프다.
(2)
그래프의 꼭짓점들 중 a, b, c, d 와 e 혹은 f 간에는 경로가 존재하지 않는다 .
∴ 연결그래프가 아니다.
■ 완전 그래프(Complete Graph)
그래프 G = (V, E) 내에 있는 모든 꼭짓점 u, v 간에 변이 있는 그래프
예제
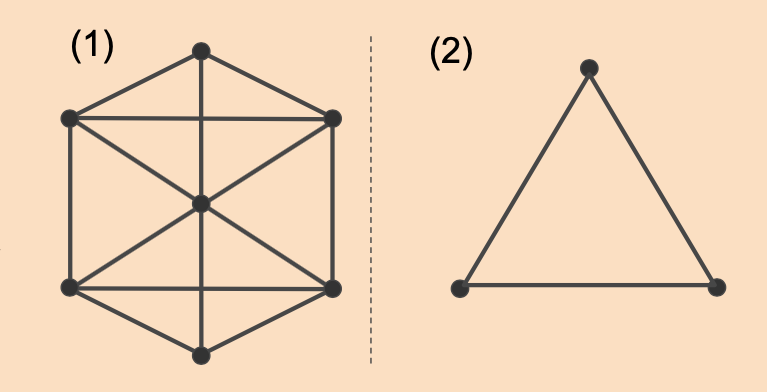
다음 중 완전 그래프인 것과 아닌 것을 구분하라.
풀이
예제풀이
(1)
모든 꼭짓점 간에 변이 존재하지 않는 것이 있다. 꼭짓점이 있다고 하면 각 꼭짓점의 차수가 같지 않다.
∴ 완전 그래프가 아니다.
(2)
모든 꼭짓점 간에 변이 존재하지 한다. 3개의 꼭짓점을 가지며 각 꼭짓점의 차수는 모두 2다.
∴ 완전 그래프이다.
■ 정규 그래프(Regular Graph)
그래프 G = (V, E) 내에 있는 모든 꼭짓점의 차수가 같은 그래프
예제
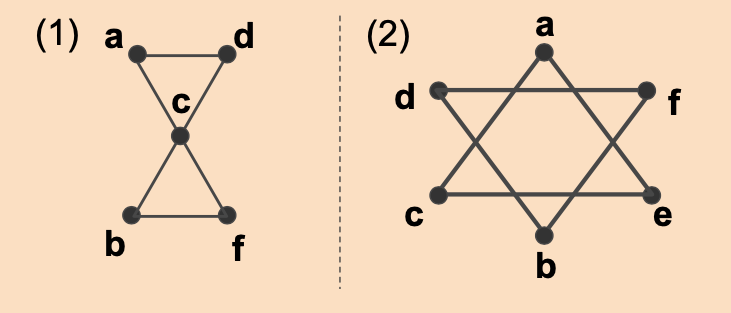
다음 중 정규 그래프인 것과 아닌 것을 구분하라.
풀이
예제풀이
(1)
모든 꼭짓점 간에 변이 존재하지 않는 것이 있다. 꼭짓점이 있다고 하면 각 꼭짓점의 차수가 같지 않다.
∴ 정규 그래프가 아니다.
(2)
d(c)=4이고 나머지 꼭짓점의 차수는 모두 2다.
∴ 2-정규 그래프이다.
■ 이분 그래프(Bipartite Graph)
그래프 내의 꼭짓점 집합을 분할(Partition)하고, 분할로 만들어진 서로 다른 꼭짓점 집합류 사이에 변이 존재하면 이분 그래프라고 합니다.
■ 완전이분 그래프(Complete Bipartite Graph)
수학으로 이해하는 디지털 논리 이산수학 314p 참고
-----------------------------------
-----------------------------------
'컴퓨터 공학 > Software Math' 카테고리의 다른 글
| [이산수학]인접행렬, 인접리스트로 그래프 표현하기 (0) | 2020.08.10 |
|---|---|
| [이산수학]해밀턴 그래프란?(예제포함) (1) | 2020.08.10 |
| [이산수학]오일러 그래프 정의와 정리(예제포함) (2) | 2020.08.09 |
| [이산수학]그래프의 종류1(부분 그래프, 부분신장 그래프, 동형 그래프, 평면 그래프) (0) | 2020.08.09 |
| [이산수학]다중그래프, 방향그래프, 가중치그래프란?(예제포함) (0) | 2020.08.09 |




댓글