반응형
해밀턴 그래프의 정의/예제포함
수학자 해밀턴은 그래프 이론을 이용해 어떤 길(변)을 지나든지 상관없이 모든 지역(꼭짓점)을 반드시 한 번씩만 지나도록 하는 방법을 연구했습니다.
■ 해밀턴 경로(Hamiltonian Path)
그래프 G = (V, E)의 모든 꼭짓점을 꼭 한 번씩 지나는 경로
■ 해밀턴 회로 / 순환( Hamiltonian Circuit /Hamiltonian Cycle)
그래프 G = (V, E)의 꼭짓점 v에서 시작해 모든 꼭짓점을 꼭 한 번씩만 지나 v로 돌아오는 회로
■ 해밀턴 그래프(Hamiltonian Graph)
해밀턴 회로를 포함하는 그래프 G = (V, E)
예제
다음 그래프에서 해밀턴 경로나 해밀턴 회로가 있는지 밝혀라.
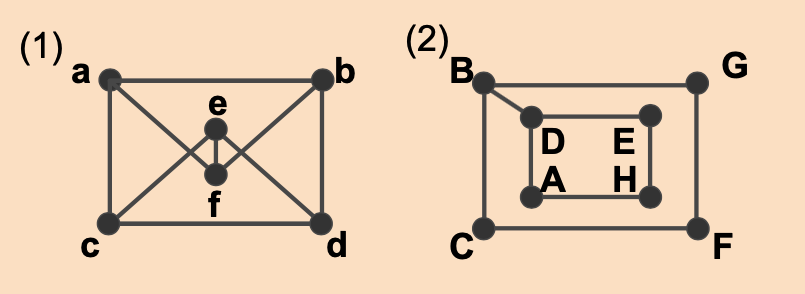
풀이
더 보기를 클릭하세요.
더보기
예제보기
(1)
해밀턴 경로의 예: a - b - c - f - d - c
해밀턴 회로의 예: a - f - d - c - e - b - a
∴ 해밀턴 경로와 해밀턴 회로 모두 존재한다.
(2)
해밀턴 경로의 예: C - F - G - B - C - A - H - E
해밀턴 회로의 경우, B 또는 D를 두 번씩 지나야 하기 때문에 존재할 수 없다.
∴ 해밀턴 경로만 존재한다.
수학으로 이해하는 디지털 논리 이산수학 325p 참고
-----------------------------------
-----------------------------------
반응형
'컴퓨터 공학 > Software Math' 카테고리의 다른 글
| [이산수학]최단경로 문제, 깊이 우선 탐색, 너비 우선 탐색이란? (예제포함) (0) | 2020.08.10 |
|---|---|
| [이산수학]인접행렬, 인접리스트로 그래프 표현하기 (0) | 2020.08.10 |
| [이산수학]그래프의 종류2(연결 그래프, 완전 그래프, 정규 그래프, 이분 그래프) (0) | 2020.08.09 |
| [이산수학]오일러 그래프 정의와 정리(예제포함) (2) | 2020.08.09 |
| [이산수학]그래프의 종류1(부분 그래프, 부분신장 그래프, 동형 그래프, 평면 그래프) (0) | 2020.08.09 |




댓글