오일러 공식에 대한 정리
연결된 평면 그래프 G에서 꼭짓점 수를 v, 변의 수를 e, 면의 수를 s라고 할 때 다음 오일러 공식이 성립합니다.
v - e + s = 2
증명
위의 공식을 증명하기 위해서는 변이 하나인 그래프와 둘 이상인 그래프를 나누어 고려해야 한다.
(1) 변이 하나인 그래프는 다음과 같이 두 종류이다.
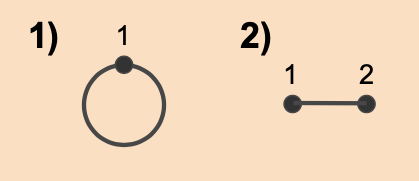
1) v = 1, e = 1. s = 2 로 v - e + s = 1 - 1 + 2 = 2
∴ 오일러 공식이 성립한다.
2) v = 2, e = 1. s = 1 로 v - e + s = 2 - 1 + 1 = 2
∴ 오일러 공식이 성립한다.
(2) 둘 이상의 변으로 구성된 그래프는 수학적 귀납법을 이용해 증명한다.
e = 1일 때, v - e + s = 2 - 1 + 1 = 2므로 오일러 공식이 성립한다. e = k일 때, v - k + s = 2로 오일러 공식이 성립한다고 가정하고, e = k +1 일 때 오일러 공식이 성립하는지 증명한다. e = k인 그래프에서 변을 추가해서 ( e = k +1 ) 얻는 평면 그래프는 다음과 같이 두 가지 경우가 있다.

(v + 1) - (k + 1) + s = v + 1 - k - 1 + s = v - k + s = 2 (∵ 귀납 가정이 성립)
∴ 오일러 공식이 성립한다.

v - (k +1) + (s + 1) = v - k - 1 + s +1
v - k + s = 2 (∵ 귀납 가정이 성립)
∴ 오일러 공식이 성립한다.
수학으로 이해하는 디지털 논리 이산수학 312p 참고
-----------------------------------
-----------------------------------
'컴퓨터 공학 > Software Math' 카테고리의 다른 글
| [이산수학]부분순서관계란? (비교가능/비교불가능/완전순서) (2) | 2020.08.21 |
|---|---|
| [이산수학] 추이폐포와 연결관계 (0) | 2020.08.21 |
| [이산수학]그래프에서 차수란?(외차수, 내차수 구하는 예제 포함) (0) | 2020.08.12 |
| [이산수학]최단경로 문제, 깊이 우선 탐색, 너비 우선 탐색이란? (예제포함) (0) | 2020.08.10 |
| [이산수학]인접행렬, 인접리스트로 그래프 표현하기 (0) | 2020.08.10 |



댓글