반응형
■ 추이폐포(Transitive Closure)
집합 A에 대해, 관계 R를 포함하면서 추이관계를 갖는 관계 S
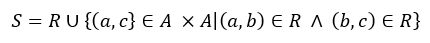
추이페포를 구하는 과정에서 새로운 순서쌍이 생기기 때문에 앞서 다룬 반사폐포나 대칭폐포를 구하는 것보다 복잡합니다.
예를 들어
집합 A = {1, 2, 4}
집합 A에 대한 관계 R = {(1,1),(1,4),(2,1),(4,2)}
위의 두 요건을 이용해 추이페포 S를 구해보겠습니다.
(2,1)이 관계 R에 존재하고, (1, 4) 또한 존재합니다. 추이폐포가 되기 위해서는 (2,1)의 앞의 원소 2와 (1,4)의 뒤의 원소인 4으로 만들어진 순서쌍 (2, 4)이 추가되어야 합니다. 이제는 (2, 4)에 대해서도 추이폐포가 되도록 순서쌍을 추가해야 합니다. 즉 관계 R에 (2,4)도 있고, (4,2)도 있으니까 (4, 4)와 (2,2)를 추가해야 합니다.
이렇게 추가되는 순서쌍에 대해서도 추이관계가 성립하는지 판별하여 추이폐포가 될 때까지 순서쌍을 추가해야 합니다. 순서쌍 원소 하나한의 추이관계를 찾는 것은 생각보다 쉽지 않습니다. 이제 추이폐포를 만들기 위한 간단한 방법을 보겠습니다.
■ 연결관계(Connectivity Relation)
원소의 개수가 n인 집합 A에 대한 관계 R에 대하여,
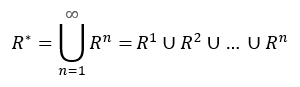
수학으로 이해하는 디지털 논리 이산수학 240p 참고
-----------------------------------
-----------------------------------
반응형
'컴퓨터 공학 > Software Math' 카테고리의 다른 글
| [이산수학]선형과 비선형, 순환과 비순환의 차이는? (0) | 2020.08.24 |
|---|---|
| [이산수학]부분순서관계란? (비교가능/비교불가능/완전순서) (2) | 2020.08.21 |
| [이산수학]꼭짓점, 변, 면과의 관계는? (오일러 공식에 대한 정리, v-e+s=2) (0) | 2020.08.13 |
| [이산수학]그래프에서 차수란?(외차수, 내차수 구하는 예제 포함) (0) | 2020.08.12 |
| [이산수학]최단경로 문제, 깊이 우선 탐색, 너비 우선 탐색이란? (예제포함) (0) | 2020.08.10 |


댓글