그래프의 활용: 최단경로 문제, 깊이 우선 탐색, 너비 우선 탐색
■ 최단경로 문제(Shortest Path Problem)
|E| > 0 인 그래프 G = (V, E)에서 꼭짓점 a, b ∈ V 간의 가장 짧은 거리의 경로를 찾는 문제
출발점(Source): 경로의 시작점
도착점(Destination): 경로의 목적지
최단경로를 구할 때는 출발점부터 도착점까지 경로에 포함되는 꼭짓점들을 나열하고, 각 변 혹은 화살표에 부여된 가중치를 더하여 가장 적은 가중치의 합을 갖는 경로를 선택합니다. 이 때 다익스트라 알고리즘을 사용할 수 있습니다. 다익스트라 알고리즘은 시작점으로부터 최단경로를 갖는 점들을 차례로 탐색해가는 알고리즘입니다 .
다음과 같은 가중치 그래프를 예로 들어보겠습니다.

■ 깊이 우선 탐색(Depth First Search)
어떤 꼭짓점에 인접한 꼭짓점에서 아직 탐색되지 않은, 왼쪽에 있는 꼭짓점을 먼저 탐색하는 방법
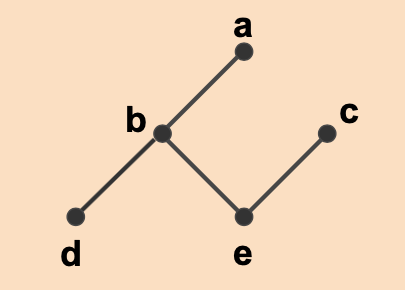
위 그래프를 깊이 우선 탐색해보겠습니다.
(1) a와 인접하고 아직 탐색되지 않은 꼭짓점 b와 c가 있다. b를 먼저 탐색한다.
∴ a - b
(2) b와 인접하고 탐색되지 않은 꼭짓점 d와 e가 있다. d를 먼저 탐색한다.
∴ a - b - d
(3) d와 인접하고 아직 탐색되지 않은 꼭짓점이 없으므로 다시 d로 돌아간다.
∴ a - b - d - e
(4) e와 인접하고 탐색되지 않은 꼭짓점 c가 있다. c를 탐색한다.
∴ a - b - d - e - c
위의 예에서 볼 수 있듯이 깊이 우선 탐색은 아래로만 탐색하는 것이 아닙니다. 탐색되지 않은 꼭짓점 중 가장 왼쪽에 위치하고 있는 꼭짓점을 먼저 탐색합니다.
예제
다음 그래프를 꼭짓점 A에서 시작하여 깊이 우선 탐색하세요.

풀이
예제풀이
(1) A와 인접하고 아직 탐색되지 않은 꼭짓점 B와 C가 있다. B를 먼저 탐색한다.
∴ A - B
(2) B와 인접하고 아직 탐색되지 않은 꼭짓점 D와 E가 있다. D를 먼저 탐색한다.
∴ A - B - D
(3) D와 인접하고 아직 탐색되지 않은 꼭짓점 G가 있다. G를 탐색한다.
∴ A - B - D - G
(4) G와 인접하고 아직 탐색되지 않은 꼭짓점 I가 있다. I를 탐색한다.
∴ A - B - D - G - I
(5) I와 인접하고 아직 탐색되지 않은 꼭짓점 H가 있다. H를 탐색한다.
∴ A - B - D - G - I - H
(6) H와 인접하고 아직 탐색되지 않은 꼭짓점 E와 F가 있다. E를 먼저 탐색한다.
∴ A - B - D - G - I - H - E
(7) E와 인접하고 아직 탐색되지 않은 꼭짓점 C가 있다. C를 탐색한다.
∴ A - B - D - G - I - H - E - C
(8) C와 인접하고 아직 탐색되지 않은 꼭짓점 F가 있다. F를 탐색한다.
∴ A - B - D - G - I - H - E - C - F
■ 너비 우선 탐색(Breath First Search)
어떤 꼭짓점에 인접한 꼭짓점을 모두 탐색한 후 탐색했던 꼭짓점들에 인접한 꼭짓점들을 차례로 탐색하는 방법

위 그래프를 깊이 우선 탐색해보겠습니다.
(1) a와 인접하고 아직 탐색되지 않은 꼭짓점 b와 c가 있다. b부터 탐색하고, c를 탐색한다.
∴ a - b - c
(2) b와 인접하고 탐색되지 않은 꼭짓점 d와 e가 있다. d부터 탐색하고, e를 탐색한다.
∴ a - b - c - d - e
(3) c와 인접하고 아직 탐색되지 않은 꼭짓점이 없다.
깊이 우선 탐색과 마찬가지로, 너비 우선 탐색도 꼭짓점 v에 인접한 꼭짓점이 하나 이상인 경우 왼쪽에 위치한 꼭짓점부터 탐색합니다.
예제
다음 그래프를 꼭짓점 A에서 시작하여 너비 우선 탐색하세요.

풀이
예제풀이
(1) A와 인접하고 아직 탐색되지 않은 꼭짓점 B와 C가 있다. B부터 탐색하고, C를 탐색한다.
∴ A - B - C
(2) B와 인접하고 탐색되지 않은 꼭짓점 D와 E가 있다. D부터 탐색하고, E를 탐색한다.
∴ A - B - C - D - E
(3) C와 인접하고 탐색되지 않은 꼭짓점 F가 있다. F를 탐색한다.
∴ A - B - C - D - E - F
(4) C와 인접하고 탐색되지 않은 꼭짓점 G가 있다. G를 탐색한다.
∴ A - B - C - D - E - F - G
(5) C와 인접하고 탐색되지 않은 꼭짓점 H가 있다. H를 탐색한다.
∴ A - B - C - D - E - F - G - H
(6) H와 인접하고 탐색되지 않은 꼭짓점이 없다.
(7) G와 인접하고 탐색되지 않은 꼭짓점 I가 있다. I를 탐색한다.
∴ A - B - C - D - E - F - G - H - I
(8) H와 인접하고 탐색되지 않은 꼭짓점이 없다.
(9) I와 인접하고 탐색되지 않은 꼭짓점이 없다.
수학으로 이해하는 디지털 논리 이산수학 336p - 344p 참고
-----------------------------------
-----------------------------------
'컴퓨터 공학 > Software Math' 카테고리의 다른 글
| [이산수학]꼭짓점, 변, 면과의 관계는? (오일러 공식에 대한 정리, v-e+s=2) (0) | 2020.08.13 |
|---|---|
| [이산수학]그래프에서 차수란?(외차수, 내차수 구하는 예제 포함) (0) | 2020.08.12 |
| [이산수학]인접행렬, 인접리스트로 그래프 표현하기 (0) | 2020.08.10 |
| [이산수학]해밀턴 그래프란?(예제포함) (1) | 2020.08.10 |
| [이산수학]그래프의 종류2(연결 그래프, 완전 그래프, 정규 그래프, 이분 그래프) (0) | 2020.08.09 |




댓글