반응형
이산수학_증명_직접증명법_명제 변형하지 않고 증명하는 법
직접증명법(Direct Proof)은 명제를 변형하지 않고 증명하는 방법입니다.
주어진 명제를 참이라고 가정하고 정리와 공리를 이용해 명제가 참이 됨을 증명합니다.
예제1 두 홀수의 곱이 홀수임을 증명하라.
p : 두 수 m, n은 홀수이다
q : mn은 홀수이다
p→q : 두 홀수 m, n의 곱은 홀수이다

∴ 명제 p→q "두 홀수 m, n의 곱은 홀수이다"는 참이다.
예제2 모든 정수 n에 대해 n이 짝수면, n^2도 짝수임을 증명하라
p : 정수 n은 짝수이다
q : n^2도 짝수이다
p→q : 정수 n은 짝수이면, n^2도 짝수이다
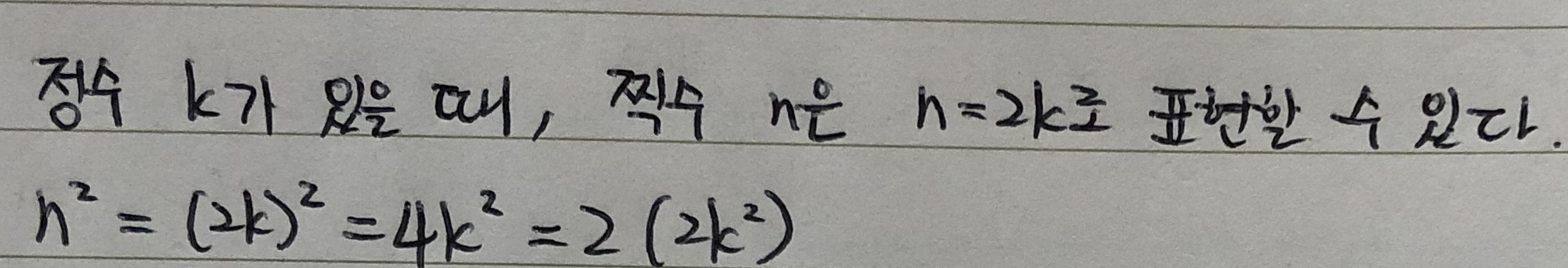
∴ 명제 p→q "정수 n은 짝수이면, n^2도 짝수이다"는 참이다.
예제3 두 유리수의 합이 유리수임을 증명하라
p : 두 수 m, n은 유리수이다
q : m,n의 합은 유리수이다
p→q : 두 유리수 m, n의 합은 유리수이다

∴ " 두 유리수 m, n의 합은 유리수이다 "는 참이다.
-----------------------------------
-----------------------------------
반응형
'컴퓨터 공학 > Software Math' 카테고리의 다른 글
| [이산수학] 수의 연산_합의 표시 ∑, 곱의 표시 ∏, 나누기ㅣ, 나머지 mod 의 뜻은? (384) | 2020.07.29 |
|---|---|
| [이산수학]간접증명법이란?(대우증명, 모순증명, 반례증명, 존재증명) (404) | 2020.07.29 |
| [이산수학]공리, 정의, 정리, 증명이란?_다양한 예로 이해하기 (388) | 2020.07.29 |
| [이산수학]한정자(Quantifier)란? 기호∀와 ∃의 의미 (403) | 2020.07.29 |
| [이산수학]논리적 동치(Logical Equivalence)/동치법칙이란? (417) | 2020.07.29 |

댓글