이산수학 이항관계(Binary), n항관계(n-ary), 역관계(Inverse)란?
■ 이항관계(Binary Relation)
집합 A, B가 있을 때, 집합 A에서 집합 B로 가는 관계로, A × B의 부분집합
두 개의 집합 A, B에 속하는 원소들 중 a∈A와 b∈B 간에 관계가 존재할 때, 이러한 관계를 이항관계라고 합니다. 이 이항관계에 포항되는 순서쌍들은 학생 정보 집합의 곱집합의 부분집합입니다.
예제
집합 A = {1, 2}, 집합 B = {a, b, c} 일 때, A에서 B로 가는 가능한 관계 R를 구하라.
풀이
예제풀이
집합 A와 집합 B 간의 가능한 관계 R은 A × B 집합이다.
∴ A × B = {(1, a),(1, b),(1, c),(2, a),(2, b),(2, c)}
■ n항관계(n-ary Relation)

관계를 갖는 집합이 셋 이상일 때, 그 집합들은 n항관계를 갖는다고 합니다. n항관계에서 갖는 순서쌍은 n개의 원소로 구성됩니다. 이항관계는 두 집합 간의 관계여서 순서쌍을 구성하는 원소가 두 개였습니다. 3항관계라면 3개, 4항관계라면 4개의 원소로 순서쌍이 구성됩니다.
예제
집합 A = {2, 3}, 집합 B = {C언어, JAVA}, 집합 C = {이초롱, 김방긋} 일 때, 이 세 집합 사이에 가능한 관계 R를 구하라.
풀이
예제풀이
A × B × C = {(2, C언어, 이초롱), (2, C언어, 김방긋),(2, JAVA, 이초롱), (2, JAVA, 김방긋),
(3, C언어, 이초롱), (3, C언어, 김방긋),(3, JAVA, 이초롱), (3, JAVA, 김방긋)}
■ 역관계(Inverse Relation)
집합 A에서 집합 B로 가는 관계에 관계 R이 있을 때, R에 대한 역관계

역관계는 관계 R이 존재해야만 만들어질 수 있는 관계입니다. 따라서 관계가 존재하지 않는 집합 간에는 역관계도 존재하지 않습니다.
예제


풀이
예제풀이
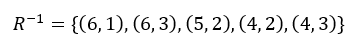
수학으로 이해하는 디지털 논리 이산수학 206-209p 참고
-----------------------------------
-----------------------------------
'컴퓨터 공학 > Software Math' 카테고리의 다른 글
| [이산수학]관계의 성질이란?(반사, 비반사, 대칭, 추이) (0) | 2020.07.30 |
|---|---|
| [이산수학]관계의 표현 종류(화살표선도,좌표도표,관계행렬,방향그래프) (0) | 2020.07.30 |
| [이산수학]관계의 정의역(Domain), 공변역(Codomain), 치역(Range)이란?_예제포함 (0) | 2020.07.30 |
| [이산수학]행렬식이란?2차, 3차 구하는 법(소행렬, 소행렬식, 여인수, 여인수행렬 개념까지) (710) | 2020.07.30 |
| [이산수학]행렬의 종류(영행렬, n차 정사각행렬, 대각행렬, 단위행렬, 전치행렬, 대칭행렬, 부울행렬) (1) | 2020.07.30 |



댓글