 [이산수학]관계의 성질이란?(반사, 비반사, 대칭, 추이)
[이산수학]관계의 성질이란?(반사, 대칭, 추이) 반사 성질에 따라 ■ 반사관계(Reflexive Relation) 모든 a ∈ A에 대해 (a, a) ∈ R인 관계 집합 A에 대한 관계 R이 반사관계가 성립하려면 집합 A의 모든 원소가 자기 자신과 대응하는 순서쌍을 가지고 있어야 합니다. 예를 들어 집합 A = {1, 2, 3} 에 대한 관계 R이 반사관계가 되려면 순서쌍 (1, 1), (2, 2), (3, 3)이 모두 관계 R의 원소로 포함되어 있어야 합니다. ■ 비반사관계 (Irreflexive Relation 모든 a ∈ A에 대해 (a, a) ∉ R인 관계 집합 A에 포함된 모든 원소에 대해 (a. a)가 관계 R에 존재하지 않는 관계입니다. 그러므로 집합 A에 포함되는 원소 중 하나라도 (a,..
2020. 7. 30.
[이산수학]관계의 성질이란?(반사, 비반사, 대칭, 추이)
[이산수학]관계의 성질이란?(반사, 대칭, 추이) 반사 성질에 따라 ■ 반사관계(Reflexive Relation) 모든 a ∈ A에 대해 (a, a) ∈ R인 관계 집합 A에 대한 관계 R이 반사관계가 성립하려면 집합 A의 모든 원소가 자기 자신과 대응하는 순서쌍을 가지고 있어야 합니다. 예를 들어 집합 A = {1, 2, 3} 에 대한 관계 R이 반사관계가 되려면 순서쌍 (1, 1), (2, 2), (3, 3)이 모두 관계 R의 원소로 포함되어 있어야 합니다. ■ 비반사관계 (Irreflexive Relation 모든 a ∈ A에 대해 (a, a) ∉ R인 관계 집합 A에 포함된 모든 원소에 대해 (a. a)가 관계 R에 존재하지 않는 관계입니다. 그러므로 집합 A에 포함되는 원소 중 하나라도 (a,..
2020. 7. 30.
 [이산수학]관계의 유형_이항관계(Binary), n항관계(n-ary), 역관계(Inverse)란?_예제포함
이산수학 이항관계(Binary), n항관계(n-ary), 역관계(Inverse)란? ■ 이항관계(Binary Relation) 집합 A, B가 있을 때, 집합 A에서 집합 B로 가는 관계로, A × B의 부분집합 두 개의 집합 A, B에 속하는 원소들 중 a∈A와 b∈B 간에 관계가 존재할 때, 이러한 관계를 이항관계라고 합니다. 이 이항관계에 포항되는 순서쌍들은 학생 정보 집합의 곱집합의 부분집합입니다. 예제 집합 A = {1, 2}, 집합 B = {a, b, c} 일 때, A에서 B로 가는 가능한 관계 R를 구하라. 풀이 더보기 예제풀이 집합 A와 집합 B 간의 가능한 관계 R은 A × B 집합이다. ∴ A × B = {(1, a),(1, b),(1, c),(2, a),(2, b),(2, c)} ■ ..
2020. 7. 30.
[이산수학]관계의 유형_이항관계(Binary), n항관계(n-ary), 역관계(Inverse)란?_예제포함
이산수학 이항관계(Binary), n항관계(n-ary), 역관계(Inverse)란? ■ 이항관계(Binary Relation) 집합 A, B가 있을 때, 집합 A에서 집합 B로 가는 관계로, A × B의 부분집합 두 개의 집합 A, B에 속하는 원소들 중 a∈A와 b∈B 간에 관계가 존재할 때, 이러한 관계를 이항관계라고 합니다. 이 이항관계에 포항되는 순서쌍들은 학생 정보 집합의 곱집합의 부분집합입니다. 예제 집합 A = {1, 2}, 집합 B = {a, b, c} 일 때, A에서 B로 가는 가능한 관계 R를 구하라. 풀이 더보기 예제풀이 집합 A와 집합 B 간의 가능한 관계 R은 A × B 집합이다. ∴ A × B = {(1, a),(1, b),(1, c),(2, a),(2, b),(2, c)} ■ ..
2020. 7. 30.
[이산수학]관계의 정의역(Domain), 공변역(Codomain), 치역(Range)이란?_예제포함
[이산수학]관계의 정의역(Domain), 공변역(Codomain), 치역(Range)이란? ■ 정의역(Domain) 집합 A에서 집합 B로 가는 이항관계 R에 속한 순서쌍의 첫 번째 원소가 포함되어 있는 집합, 즉 집합 A dom(R) = {a|a ∈ A} ■ 공변역(Codomain) 집합 A에서 집합 B로 가는 이항관계 R에 속한 순서쌍의 두 번째 원소가 포함되어 있는 집합, 즉 집합 B codom(R) = {b|b ∈ A} ■ 치역(Range) 집합 A에서 집합 B로 가는 관계 R에 속한 순서쌍의 두 번째 원소들을 모아놓은 집합, 공변역의 부분집합 ran(R) = {b|(a, b) ∈ R} ⊆ B 예제 집합 A = {x|1 ≤ x ≤ 5, x는 정수} 일 때, A에서 A로 가는 관계 R은 다음과 같다..
2020. 7. 30.
[이산수학]집합의 종류는?(공집합, 부분집합, 진부분집합)
이산수학 집합의 종류는?(공집합, 부분집합, 진부분집합) ■ 전체집합(Universal Set) : 논의 대상이 되는 원소 전체를 포함하는 집합, U 예로 집합 A가 다음과 같다고 하면, A = {x | x > 13, x ∈ N} 집합 A는 원소 x를 가지는데, x는 13보다 큰 자연수입니다. 즉 집합 A는 자연수 중 13보다 큰 자연수의 집합이며, 집합 A를 포함하는 전체집합은 자연수집합(N)이 됩니다. ■ 공집합(Empty Set) : 하나의 원소도 포함하지 않는 집합, ∅ 또는 { } |∅| = 0 공집합은 어떠한 원소도 포함하지 않기 때문에 공집합의 기수는 항상 0입니다. ■ 부분집합(SubSet) - 집합 A의 모든 원소가 집합 B에 포함되는 경우, |A| ≤ |B| - A와 B가 상등이거나, ..
2020. 7. 29.
 [이산수학]역(Converse), 이(Inverse), 대우(Contraposition)이란?_진리표첨부
이산수학_명제와논리_역(Converse), 이(Inverse), 대우(Contraposition)이란? 때로는 주어진 명제만으로 논리를 전개하거나 증명하기가 어려울 때가 있습니다. 이때 역, 이, 대우 중 하나를 이용하면 쉽게 해결할 수 있습니다. 간접증명할 때 사용하기도 합니다. ■ 역, 이, 대우 진리표 빨간네모: 대우명제는 본 명제와 같은 진릿값을 갖습니다. 파란네모: 역명제는 이명제와 같은 진릿값을 갖습니다. ■ 연습문제 명제 "오늘 눈이 오면 나는 치킨을 먹는다."의 역, 이, 대우를 구해봅시다. p: 오늘 눈이 온다. q: 나는 치킨을 먹는다. 역: 내가 치킨을 먹으면 눈이 온다. 이: 오늘 눈이 오지 않으면, 나는 치킨을 먹지 않는다. 대우: 내가 치킨을 먹지 않으면, 오늘 눈이 오지 않는다..
2020. 7. 29.
[이산수학]역(Converse), 이(Inverse), 대우(Contraposition)이란?_진리표첨부
이산수학_명제와논리_역(Converse), 이(Inverse), 대우(Contraposition)이란? 때로는 주어진 명제만으로 논리를 전개하거나 증명하기가 어려울 때가 있습니다. 이때 역, 이, 대우 중 하나를 이용하면 쉽게 해결할 수 있습니다. 간접증명할 때 사용하기도 합니다. ■ 역, 이, 대우 진리표 빨간네모: 대우명제는 본 명제와 같은 진릿값을 갖습니다. 파란네모: 역명제는 이명제와 같은 진릿값을 갖습니다. ■ 연습문제 명제 "오늘 눈이 오면 나는 치킨을 먹는다."의 역, 이, 대우를 구해봅시다. p: 오늘 눈이 온다. q: 나는 치킨을 먹는다. 역: 내가 치킨을 먹으면 눈이 온다. 이: 오늘 눈이 오지 않으면, 나는 치킨을 먹지 않는다. 대우: 내가 치킨을 먹지 않으면, 오늘 눈이 오지 않는다..
2020. 7. 29.
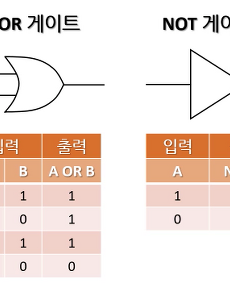 [이산수학]논리게이트(Logit Gate)란? 게이트의 종류(AND,OR, NOT,NAND,NOR,XOR)
[이산수학]논리게이트(Logit Gate)란? 게이트의 종류(AND,OR, NOT,NAND,NOR,XOR) 디지털 회로를 만들려면 정확한 연산 과정을 표현하는 논리회로(logit circuit)가 필요합니다. 연산 과정을 회로로 표현할 때 논리게이트(Logic Gate)를 이용합니다. 논리 게이트는 하나 이상의 2진 입렵 정보를 받아 하나의 2진 출력 정보를 갖습니다. ■ 논리 회로(logit circuit) -논리 연산을 통해 전기 장치를 제어하는 통로 -컴퓨터 및 기타 전기 장치를 작동하게 만드는 기초 부품 -불 대수를 이용하여 설계 -여러 입력을 해도 출력 1개만 나온다. ■ 게이트(gate) -논리 회로의 기초 구성요소 -각 게이트는 불 연산 하나를 구현 -데이터 저장 기능은 없음 ■ 기본게이트 ..
2020. 7. 29.
[이산수학]논리게이트(Logit Gate)란? 게이트의 종류(AND,OR, NOT,NAND,NOR,XOR)
[이산수학]논리게이트(Logit Gate)란? 게이트의 종류(AND,OR, NOT,NAND,NOR,XOR) 디지털 회로를 만들려면 정확한 연산 과정을 표현하는 논리회로(logit circuit)가 필요합니다. 연산 과정을 회로로 표현할 때 논리게이트(Logic Gate)를 이용합니다. 논리 게이트는 하나 이상의 2진 입렵 정보를 받아 하나의 2진 출력 정보를 갖습니다. ■ 논리 회로(logit circuit) -논리 연산을 통해 전기 장치를 제어하는 통로 -컴퓨터 및 기타 전기 장치를 작동하게 만드는 기초 부품 -불 대수를 이용하여 설계 -여러 입력을 해도 출력 1개만 나온다. ■ 게이트(gate) -논리 회로의 기초 구성요소 -각 게이트는 불 연산 하나를 구현 -데이터 저장 기능은 없음 ■ 기본게이트 ..
2020. 7. 29.
 [이산수학]논리연산자란?(부정, 논리곱, 논리합, 배타적 논리합)_진리표로 나타내기
[이산수학]논리연산자란?(부정, 논리곱, 논리합, 배타적 논리합)_진리표로 나타내기 명제는 두 개 이상 결합하여 사용됩니다. 이 때 논리 연산자를 이용하는데 부정, 논리곱, 논리합, 배타적 논리합이 있습니다. 여러 명제를 합친 결과를 비교할 때 유용한 '진리표(Truth Table)'가 있습니다. 명제에서 나올 수 있는 참/거짓 판단의 모든 가능성을 표로 나열하였습니다. 예로 단순 명제 p의 진리표는 다음과 같습니다. ※ 단순 명제: 더 이상 나눌 수 없는 명제 p T(True, 참) F(False, 거짓) 이제 명제의 결합 중에 어떤 것이 있는지 보고, 이해를 위해 진리표와 밴다이어그램도 다루겠습니다. ■ 부정 (Negation) NOT 명제 p를 부정 예) 오늘 새로운 메뉴가 나온다. ->오늘 새로운..
2020. 7. 27.
[이산수학]논리연산자란?(부정, 논리곱, 논리합, 배타적 논리합)_진리표로 나타내기
[이산수학]논리연산자란?(부정, 논리곱, 논리합, 배타적 논리합)_진리표로 나타내기 명제는 두 개 이상 결합하여 사용됩니다. 이 때 논리 연산자를 이용하는데 부정, 논리곱, 논리합, 배타적 논리합이 있습니다. 여러 명제를 합친 결과를 비교할 때 유용한 '진리표(Truth Table)'가 있습니다. 명제에서 나올 수 있는 참/거짓 판단의 모든 가능성을 표로 나열하였습니다. 예로 단순 명제 p의 진리표는 다음과 같습니다. ※ 단순 명제: 더 이상 나눌 수 없는 명제 p T(True, 참) F(False, 거짓) 이제 명제의 결합 중에 어떤 것이 있는지 보고, 이해를 위해 진리표와 밴다이어그램도 다루겠습니다. ■ 부정 (Negation) NOT 명제 p를 부정 예) 오늘 새로운 메뉴가 나온다. ->오늘 새로운..
2020. 7. 27.
[ C ]커스텀 자료형 이해하기6_열거형(Enumerated Type)란? 개념/선언방법
C언어 열거형(Enumerated Type)란? ■ 열거형 개념, 선언방법 열겨형은 변수에 저장가능한 값을 열거하여 정의합니다. 그래서 열거형 변수명을 IndianBoy로 하고 다음과 같이 값을 넣을 수 있습니다. enum indianBoy { One=1, Two=2, Three=3, Four=4, Five=5 }; IndianBoy형 변수가 저장할 수 있는 값으로는 One, Two, Three.. 라는 상수가 있으며, 각각 1, 2, 3...으로 정의하였습니다. 이 열거형 변수를 선언하려면 구조체에 struct 키워드 붙이듯이 enum 키워드를 사용하면 됩니다. enum indianBoy song1; // indianBoy형 변수 song1선언 이제 위의 열거형을 typedef 선언을 추가해서 정의한 ..
2020. 7. 24.