[이산수학]공리, 정의, 정리, 증명이란?_다양한 예로 이해하기
이산수학_증명_공리, 정의, 정리, 증명이란?_다양한 예로 이해하기 개발자가 직접 만든 프로그램이 뛰어나다는 것을 알리기 위해 프로그램의 처리속도, 유용성, 유지보수성 등 여러 가지 검증자료를 보여주는 과정을 증명이라고 합니다. 그럼 증명하기 위해 필요한 개념들에 대해 알아보겠습니다. ■ 공리(Axiom) 별도의 증명 없이 참(T)으로 이용되는 명제 예) - 어떤 것도 포함하지 않는 집합(공집합)이 존재한다. - 어떤 자연수 n에 대해, n+1이 존재한다. - 두 점이 주어졌을 때, 그 두 점을 통과하는 직선을 그을 수 있다. ■ 정의(Definition) 논의의 대상을 보편화하기 위해 사용하는 용어 또는 기호의 의미를 확실하게 규정한 문장이나 식 예) - 한 내각의 크기가 직각인 삼각형을 직각삼각형이라..
2020. 7. 29.
 [이산수학]역(Converse), 이(Inverse), 대우(Contraposition)이란?_진리표첨부
이산수학_명제와논리_역(Converse), 이(Inverse), 대우(Contraposition)이란? 때로는 주어진 명제만으로 논리를 전개하거나 증명하기가 어려울 때가 있습니다. 이때 역, 이, 대우 중 하나를 이용하면 쉽게 해결할 수 있습니다. 간접증명할 때 사용하기도 합니다. ■ 역, 이, 대우 진리표 빨간네모: 대우명제는 본 명제와 같은 진릿값을 갖습니다. 파란네모: 역명제는 이명제와 같은 진릿값을 갖습니다. ■ 연습문제 명제 "오늘 눈이 오면 나는 치킨을 먹는다."의 역, 이, 대우를 구해봅시다. p: 오늘 눈이 온다. q: 나는 치킨을 먹는다. 역: 내가 치킨을 먹으면 눈이 온다. 이: 오늘 눈이 오지 않으면, 나는 치킨을 먹지 않는다. 대우: 내가 치킨을 먹지 않으면, 오늘 눈이 오지 않는다..
2020. 7. 29.
[이산수학]역(Converse), 이(Inverse), 대우(Contraposition)이란?_진리표첨부
이산수학_명제와논리_역(Converse), 이(Inverse), 대우(Contraposition)이란? 때로는 주어진 명제만으로 논리를 전개하거나 증명하기가 어려울 때가 있습니다. 이때 역, 이, 대우 중 하나를 이용하면 쉽게 해결할 수 있습니다. 간접증명할 때 사용하기도 합니다. ■ 역, 이, 대우 진리표 빨간네모: 대우명제는 본 명제와 같은 진릿값을 갖습니다. 파란네모: 역명제는 이명제와 같은 진릿값을 갖습니다. ■ 연습문제 명제 "오늘 눈이 오면 나는 치킨을 먹는다."의 역, 이, 대우를 구해봅시다. p: 오늘 눈이 온다. q: 나는 치킨을 먹는다. 역: 내가 치킨을 먹으면 눈이 온다. 이: 오늘 눈이 오지 않으면, 나는 치킨을 먹지 않는다. 대우: 내가 치킨을 먹지 않으면, 오늘 눈이 오지 않는다..
2020. 7. 29.
 [이산수학]논리게이트(Logit Gate)란? 게이트의 종류(AND,OR, NOT,NAND,NOR,XOR)
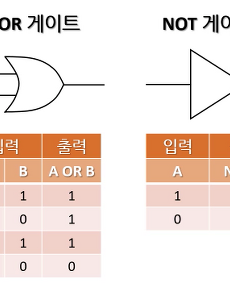
[이산수학]논리게이트(Logit Gate)란? 게이트의 종류(AND,OR, NOT,NAND,NOR,XOR) 디지털 회로를 만들려면 정확한 연산 과정을 표현하는 논리회로(logit circuit)가 필요합니다. 연산 과정을 회로로 표현할 때 논리게이트(Logic Gate)를 이용합니다. 논리 게이트는 하나 이상의 2진 입렵 정보를 받아 하나의 2진 출력 정보를 갖습니다. ■ 논리 회로(logit circuit) -논리 연산을 통해 전기 장치를 제어하는 통로 -컴퓨터 및 기타 전기 장치를 작동하게 만드는 기초 부품 -불 대수를 이용하여 설계 -여러 입력을 해도 출력 1개만 나온다. ■ 게이트(gate) -논리 회로의 기초 구성요소 -각 게이트는 불 연산 하나를 구현 -데이터 저장 기능은 없음 ■ 기본게이트 ..
2020. 7. 29.
[이산수학]논리게이트(Logit Gate)란? 게이트의 종류(AND,OR, NOT,NAND,NOR,XOR)
[이산수학]논리게이트(Logit Gate)란? 게이트의 종류(AND,OR, NOT,NAND,NOR,XOR) 디지털 회로를 만들려면 정확한 연산 과정을 표현하는 논리회로(logit circuit)가 필요합니다. 연산 과정을 회로로 표현할 때 논리게이트(Logic Gate)를 이용합니다. 논리 게이트는 하나 이상의 2진 입렵 정보를 받아 하나의 2진 출력 정보를 갖습니다. ■ 논리 회로(logit circuit) -논리 연산을 통해 전기 장치를 제어하는 통로 -컴퓨터 및 기타 전기 장치를 작동하게 만드는 기초 부품 -불 대수를 이용하여 설계 -여러 입력을 해도 출력 1개만 나온다. ■ 게이트(gate) -논리 회로의 기초 구성요소 -각 게이트는 불 연산 하나를 구현 -데이터 저장 기능은 없음 ■ 기본게이트 ..
2020. 7. 29.
 [이산수학]논리연산자란?(부정, 논리곱, 논리합, 배타적 논리합)_진리표로 나타내기
[이산수학]논리연산자란?(부정, 논리곱, 논리합, 배타적 논리합)_진리표로 나타내기 명제는 두 개 이상 결합하여 사용됩니다. 이 때 논리 연산자를 이용하는데 부정, 논리곱, 논리합, 배타적 논리합이 있습니다. 여러 명제를 합친 결과를 비교할 때 유용한 '진리표(Truth Table)'가 있습니다. 명제에서 나올 수 있는 참/거짓 판단의 모든 가능성을 표로 나열하였습니다. 예로 단순 명제 p의 진리표는 다음과 같습니다. ※ 단순 명제: 더 이상 나눌 수 없는 명제 p T(True, 참) F(False, 거짓) 이제 명제의 결합 중에 어떤 것이 있는지 보고, 이해를 위해 진리표와 밴다이어그램도 다루겠습니다. ■ 부정 (Negation) NOT 명제 p를 부정 예) 오늘 새로운 메뉴가 나온다. ->오늘 새로운..
2020. 7. 27.
[이산수학]논리연산자란?(부정, 논리곱, 논리합, 배타적 논리합)_진리표로 나타내기
[이산수학]논리연산자란?(부정, 논리곱, 논리합, 배타적 논리합)_진리표로 나타내기 명제는 두 개 이상 결합하여 사용됩니다. 이 때 논리 연산자를 이용하는데 부정, 논리곱, 논리합, 배타적 논리합이 있습니다. 여러 명제를 합친 결과를 비교할 때 유용한 '진리표(Truth Table)'가 있습니다. 명제에서 나올 수 있는 참/거짓 판단의 모든 가능성을 표로 나열하였습니다. 예로 단순 명제 p의 진리표는 다음과 같습니다. ※ 단순 명제: 더 이상 나눌 수 없는 명제 p T(True, 참) F(False, 거짓) 이제 명제의 결합 중에 어떤 것이 있는지 보고, 이해를 위해 진리표와 밴다이어그램도 다루겠습니다. ■ 부정 (Negation) NOT 명제 p를 부정 예) 오늘 새로운 메뉴가 나온다. ->오늘 새로운..
2020. 7. 27.